1. Lintasan benda berupa lingkaran
2. Jarak partikel ke titik acuan selalu tetap
3. Kelajuan selalu tetap
4. Kecepatan selalu berubah arah
5. Besar kecepatan tetap
6. Mempunyai percepatan sentripetal yang mengarah ke pusat lintasan
Besaran-besaran yang terdapat pada GMB
1. Periode dan frekuensi
2. Kecepatan linier
3. Kecepatan anguler (kecepatan sudut)
4. Percepatan sentripetal yang mengarah ke pusat lintasan
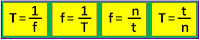
T = Periode yaitu waktu yang diperlukan untuk menempuh satu putaran
f = Frekuensi yaitu banyaknya putaran yang terjadi selama satu detik
v = kecepatan linier yaitu perpindahan materi yang bergerak melingkar tiap satuan waktu
w = kecepatan sudut yaitu sudut yang disapu (ditempuh) tiap satuan waktu
4. Percepatan sentripetal yang mengarah ke pusat lintasan
T = Periode yaitu waktu yang diperlukan untuk menempuh satu putaran
f = Frekuensi yaitu banyaknya putaran yang terjadi selama satu detik
v = kecepatan linier yaitu perpindahan materi yang bergerak melingkar tiap satuan waktu
w = kecepatan sudut yaitu sudut yang disapu (ditempuh) tiap satuan waktu
DEFINISI SATU RADIAN
1 Radian = 1 Rad = adalah sudut yang ditempuh oleh titik materi dimana panjang lintasan yang ditempuh sama dengan panjang jari-jari lingkaran.
perhatika gambar di bawah ini bahwa jari jari R = busur AB
RUMUS-RUMUS PADA GMB
1 Radian = 1 Rad = adalah sudut yang ditempuh oleh titik materi dimana panjang lintasan yang ditempuh sama dengan panjang jari-jari lingkaran.
perhatika gambar di bawah ini bahwa jari jari R = busur AB
RUMUS-RUMUS PADA GMB
PERCEPATAN SENTRIPETAL PADA GMB
Percepatan sentripetal pada gerak melingkar beraturan mempunyai arah menuju pusat lingkaran. Persamaan percepatan sentripetal dapat daicari dari perbandingan kesebangunan vektor kecepatan dan perpindahan materi. Pada kehidupan sehari hari arah percepatan sentripetal biasa kita rasakan ketika kita bersepeda dan menikung pada lintasan yang berbelok.
as = percepatan sentripetal
v = kecepatan linier
R = jari jari lintasan
Gerak Melingkar Beraturan (GMB) adalah gerakan dalam lintasan berbentuk lingkaran dengan percepatan sudut tetap.
Beberapa lambang yang biasa ditemukan dalam GMB antara lain :
Frekuensi (f) dan periode (T) dalam GMB :
sesuai dengan keterangan lambang2 di atas berarti :
Frekuensi = banyaknya putaran/waktu
Periode = waktu/banyaknya putaran
Rumus Kecepatan Sudut (ω)

Keterangan :
ω = Kecepatan sudut (rad/s)
f = frekuensi (Hz)
T = periode (s)
π = 3,14 atau 22/7 atau tetap/tidak diganti angka
Hubungan Kecepatan Sudut dan Kecepatan Linear :
Percepatan dan Gaya Sentripetal :
percepatan sentripetal merupakan percepatan benda menuju pusat lingkaran....adanya percepatan ini menimbulkan gaya sentripetal.
Benda Yang Diputar Horizontal
mempunyai kecepatan maksimum (vmaks) yang dibatasi oleh tegangan tali maksimum (Tmaks) agar talinya tidak sampai putus.
AyunanKerucut (Konis)
Rumus-rumus dalam ayunan kerucut :
Kelajuan maksimum agar kendaraan membelok dengan baik
Sudut Kemiringan Jalan pada Belokan :
Pentiiing......
penggunaan rumus diatas ketika yang diketahui atai yang ditanyakan adalah kecepatan liniernya....namun bila yang diketahui adalah kecepatan sudutnya maka bagian rumus dibawah ini berubah menjadi....
pada pembahasan selanjutnya kecepatan yang dipakai adalah kecepatan linear......bila ada soal yang menggunakan kecepatan sudut cukup mengganti bagian yan ditampilkan di atas.
Gerak Melingkar Vertikal pada Seutas Tali
coba kalian perhatikan gaya2 yang bekerja pada bandul di setiap titiknya.....bila menuju pusat lingkaran bernilai positif sedangkan yang menjauhi pusat bernilai negatif. pada setiap titik tegangan tali (T) selalu menuju pusat lingkaran...sehingga harganya selalu ditulis positif. Kemudian berat bandul di titik A berarah menjauhi pusat lingkaran sehingga bernilai negatif, berat bandul di titik B tegak lurus dengan tali sehingga tidak memengaruhi besarnya tegangan tali atau bernilai nol (0) dan titik C berat bandul menuju pusat lingkaran sehingga bernilai positif.....dengan melihat pengaruh berat benda pada titik sembarang....misalnya titik P.....terlihat berat benda yang mempengaruhi tegangan tali sesuai dengan perkalian berat bandul dengan nilai Cos sudut dengan acuan titik A....penggabungan besarnya tegangan dan pengaruh berat bandul setara dengan gaya sentripetal benda (Fs).
maka tegangan tali dapat kita cari dengan memindahkan pengaruh berat benda ke ruas kanan.....
kedua rumus di atas sebenarnya sama persis....hanya terjadi peruraian rumus saja terserah yang akan kalian hafal yang mana...bila sudah tahu prinsipnya sebenarnya tidak harus dihafal. sedangkan rumus2 khusus di beberapa titik sebagai berikut :
kecepatan minimum untuk.....
Gerak Melingkar Vertikal dalam Lingkaran
berbeda dengan gerak vertikal benda yang diikat dengan seutas tali......pada gerakan ini benda bergerak di dalam lintasan lingkaran yang vertikal atau dapat juga tempat berpijak bendalah yang berputar vertikal sementara benda tersebut berada di sebelah dalamnya....seperti air dalam ember yang diikat tali...atau pilot pesawat yang bermanuver membentuk lingkaran vertikal....atau seperti contoh gambar di atas (bola dalam ember). dalam kondisi ini berlaku rumus umum :
kecepatan minimal agar saat di titik tertinggi benda tidak meninggalkan lintasan.....
Gerakan Melingkar Vertikal di Luar Lingkaran
contoh gerakan ini adalah ketika sebuah kendaraan melintasi jalan yang gundukannya membentuk lingkaran....
coba kalian perhatikan....mengapa berat benda dikalikan dengan sin...dan bukannya cos.... alasannya terlihat dalam penguraian gaya berat pada gambar.... sehingga rumus umumnya :
saat di puncak berlaku.....
bahasan terakhir kita mengenai....
Hubungan Roda - roda
- Jika roda-roda sama pusatnya maka kecepatan sudutnya sama....dengan kecepatan sudut yang sama maka dapat kita cari kecepatan linier salah satu roda jika kecepatan linier roda yang lainnya diketahui.
- Jika roda-roda sama lintasannya maka kecepatan liniernya sama....dengan kecepatan linier yang sama maka dapat kita cari kecepatan sudut salah satu roda jika kecepatan sudut roda yang lainnya diketahui.


































Tidak ada komentar:
Posting Komentar